|
|
|
\require{AMSmath}

Reageren...
Re: Stelsel bij vraagstuk oplossen
In een cirkel heb ik een koorde van 10 cm breed, in het midden van de koorde is de afstand tot de cirkel 1 cm.
Hoe bereken ik de straal van deze cirkel?
Antwoord
 Beste Wouter, Beste Wouter,
Ik ga je hier niet de oplossing geven, maar wel een tip hoe je het zelf op kunt lossen. Dat geeft tenslotte de meeste voldoening. Kom je er dan echt niet uit dan kun je vraag nog een keer stellen.
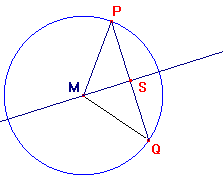
Teken de driehoek met als basis de koorde (dus dat is één zijde van de driehoek) en als ander hoekpunt het middelpunt van de cirkel. Je krijgt dan een driehoek met als één zijde de koorde en de andere twee zijden hebben de lengte van de straal van de cirkel. Deze wil je berekenen.
Teken dan de hoogtelijn van deze driehoek. Dat is in jouw geval de afstand van r-1 cm. Deze hoogtelijn staat per definitie loodrecht op de koorde, maar gaat ook precies door het midden van de koorde. Kijk maar eens waarom.
Je krijgt dan een rechthoekige driehoek waarvan de schuine zijde de lengte van de straal van de cirkel heeft en nu kun je met de stelling van Pythagoras die lengte uitrekenen.
Heel veel succes, en het lukt je nu vast!
Gebruik dit formulier alleen om te reageren op de inhoud van de vraag en/of het
antwoord hierboven. Voor het stellen van nieuwe vragen kan je gebruik maken
van een vraag stellen in het menu aan de linker kant. Alvast bedankt!
|


 Beste Wouter,
Beste Wouter,